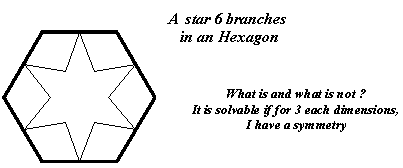
6 Differenciates Subsets
Twice (3 x 2) Different Questions
2 subsets of 3 each open their doubts in 2 registers. Difference strength there, may be something interesting in separating angle. 2 x 2 angles are right 90° (remind that perpendicular carry uncorrelation). Here 3 x 2 one to follower angle, still "sharp" is 60°. 4 x 2 (octogon) angles at 45° (half 90°) from one corner to another, then can carry linearity or equality (remind that in an orthonormal base system, x = y as a line at 45°. Higher one 5 x 2 and more, tending to smooth.

May be this 6 branch star can picture a concept of balance (or justice) and of separation, maniqueist (the good and the bad): the yes - no - doubt of both side, than could come the decision (it would be than 7).
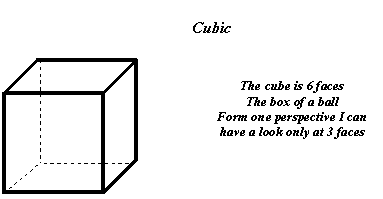
Cubic State
Object see a cube (be squared), imagine subject. Better a spheric border smooth evrywhere. Put the first in the second, square of the sphere, if your model (the square) coincide well with the subject (sphere). But that does not mean that anyone human has and should have the same perspective on a given subject. At best all see an ellipse (part of), none is the same (each cover), all are effective perspective on the sphere(scientific consistency) and all are enough shared criteria (straight cuts).
In other words, all have a (real) piece of cake, none has the same (no need to fight?), everyone see (subjectivelly) more (ellipse rather than sphere) but whatever their wish, are satisfied others are too from their piece of cake and which hope they put on it. Indeed this implies other steps. Before, for making the cake. After for eating the cake, and so on.
Anlaysis is a simplification: a cubic box within or containing the ball?
Concept of the degree of liberty: given an object how many dimensions should I know? - to know all of them in a closure, if I know the whole ?
Mind the construction of a 5 branches star. Know next top of a branch, and the rule to prolong the border, plus the other rule for get in and closure of the frame; plus the thing that 5 branchs are all equal, in different positions. Degree of liberty would be, in the minimum I know to deduce all the frame what remain I do not need to know to finish the frame. Essential to any evolving thing: how a collection of pieces and properties? - is enough to reach unit by itself and maintain, maximum complex unit. Important to formal system when the design is enough well specified for the model has a solution; probably reasonable, but (and may be more important) the model could be qualified a sustainable model.
Mind a convex object everywhere, sharp-right like the cube, smooth like the sphere. Convex means for a closed shape that there will not be punch or hole (that would be hard to calculate the optimum locally) or any right plane will always make contact by just one point with the border.
Mind what remain to know with degree of freedom. See what you want how it can be pictured. Use common sense it is not so unwise.
- A segment and a piece of the segment: dimension 1, I know the whole, I know the piece of the segment, the complement can be easilly deduced, no more I should know: zero degree of liberty
- An area and a piece of plane: dimensions 2, I know the whole, there are 3 complements, one for each each side (2 sides) of the area, up to the border of the piece of plane and the complement which is not sided (but pointed). Of this 3 complements only to know one (2 degrees of liberty) with other wholesomeness properties, 2 others can be easily deduced.
- Mind a volume, in short: dimensions 3, degree of liberty 3
This gives a sense to my lazyness (good economic mean), not any means for anything. Freedom is not to mind onself as highest God: this is crazzy; but yet to think that what I can save there can let me time to go on, care another problem, up to the end of life. So the crime of reduction, to have set itself too low in heuristics and gave the illusion that things were as simple, and the wisdom of achievment having cared enough to make things happen without having reduced the range of potential; as far as possible, in other words having done well but not too much, having let "les bons temps roulers" but not let the dikes fail.
Now what sort of degree of liberty for well delimited and well known whole ? - what you may calculate by deduction of properties. Why that for? Identify what you need to know to solve. What remain to know. But that is when things are simple. Envision what you want, see the pathways to your solutions. Mind geometrically. Think what still may be needed to know. For example, a triangle: to know all about dimensions and scale there are various formula with lengthes of sides. But also it is a plane; it could be: length of 2 sides if you know one angle. It can be only one side if knowing 2 angles... Area may not be plane, as in non Euclidean geometry you need curvatures too.
What we care for? - for that you understand that policies, things, concepts, programs are not to be taken just as points, or perfect one (1) solution. Large definition avoid contradictions while pretending to be one (1) view: the dictator of democracy should not be one person but a positive common will (may be second best option included with first best free choice). What is essential is some volumic frame to care a concern, an interest, its effects.
Human is better, with a given abstract logical volume, that could cover its transforms, manipulate as if a material object or an art and an aesthetic form it succeed to make.
Hexagon
Experts of dialectic, audience of political niceties be for populist or reasonable policies, all are pretending to have intelligent truth and gifted, to ground in that their rights for privileges, just on that with no doubt on consistency. It is not our purpose to say that citizens should stop to imagine a better world, at the bar at the corner of the street, if their populi vox could be better eared. Neither our purpose is to make people think that better to mind our moving world could be simply resumed thanks to geometric treatments. But to balance and consider approach that can:
- Lower the inflation of macro-prolific production of predictions,
- Process practices in a more modest systemic care of effects,
- Preserve the extensive culture of speculative management,
- Better anchors in cultures expressing collective intelligence,
- Enrich with open mind systemics rather than try to follow, one by one anarchy of gracefull academic abstractions,
- Take control of shameful hypocrisies pretending to mean far from any serious balanced commitment,
- Mind and support better anyone intelligent involvment (not to pretend anyone an expert of perfect intuitionist),
- Bring aids, supports with tools, diffuse essencial knowledge,
- Prevent pretention that talent should concentrate all social privileges,
- Prevent other accept the disgrace of accumulation of disadvantages.
In the expression of your skills and management it is not to pretend everyone will produce perfect definition without mistakes in their management of concepts, or they should all be considered, requirring to delegate everything to skilled people.
A Society will fill its logical space not with perfect abstract policies, only able to be minded by superior realistic individuals. It is already well clear that is better proportions could be included more or less appropriatedly in a priviledged social strata, not the most gifted and best workers are those who govern neither themselves really govern for best talented only.
So what we need is better evidence of relationships, between justice and humane wealth. Better evidences between work, intelligence responsabilities and incorporation of scientific care without producing so many inequalities and injustice. We must find better articulation and/or sequences between solidarity - freedom - diversity - humane unity; combining wealth and environmental care, since we have shown that we have or can create the means for that.
Working figurativelly closer to reality and practical envisions of what we seek and do collectivelly, allow to provide more consistent feedbacks, not too late, neither too unresponsibly transmitted to future generations.
