Operations Logics Too
Operations Reduced
Quantities are commonly made operativelly indifferent. See, term of mathematics, "function of a model", all questions are packed into parameters, scale and variable(s) and - operations are conceived perfectly neutral. Questioning the meaning of exponent (or power) or (relative) sign is avoided. So any transformations and calculus are made arbitrarily easy. There is the need to see before, while and after, how anything are and operate together. This implies definitions (qualitative) on quantifications (say quantizations?) and mind if they could change. Then how they amount together or transform. With the most natural amounts, neutral to themselves as they could be: operations applies, but they still can have different meaning. Thereafter how they define respect to others: how they interact, transform or redefine.
In the hurry to get rid of calculus, operations are made without care. Hard technosciences have indeed provided formula somehow properly covering what they mean, but "soft sciences? - do they cover properlly wht they mean despite so wildelly detailed definitions? -, more commonly they reduce and prevent to care, everything turn artificially confused. Numbers must support theories and theories are generally preferred free from complex operations to "master reality". Because, as for most common schoolchildren, it has been "so hard" to learn about numbers; this has made most of us stand on binary extremes: simple numbers & simple operations, which means no reality between, just: " what I say is true ... trust me" ( ... dude). So operations are made improperly indifferently operating and framed so. Numbers identified to something are just labels and operated, on their own, as reductivelly as possible.
Simple operations are + (add), - (less), x (multiply) or . (product) and / (div). Even = (equal) is more often taken for assignated (equalized: induced) rather than "evidenced equal" (deduced from). Most people dyslike exponent or power, integration or derivation. Not to speak of operators, despite they could be a start to something modular and complex (in en explicit identified way and out some "periodicians"). With some care, complexity could have good use of more careful specifications of numbers and operations. Starting by paying some attention to theoretical preliminaries of pure mathematics. They: in fact and for practice, are just the conditions of application of accounting systems or algebra. Care that, knowing about constraints of purity can show you how improperly are used formal tools, but could have many other good uses.
For example; basis, which start analytic systems of numbers is intuitive. In most case made of zero and unit (0,1). From time to time, philosophical concern came up as the need to examine basic significance like of zero (0). Civilizations found sometime hard to discover it (why an empty symbolized ?). Complex unit, ( could we suggest ?) must "emerge". Our suggestion is with logarithm: the logarithm of unit is zero. After which, quantity (amount) turns positivelly existing. While before parts do not make unit (or base). In logarithm they are negative (not yet unit) as with their log previous to one.
There could be 2 important reasons to be more cautious and mind it a little bit. First computer does what you input and deliver any number. Not necessarilly checking its consistency, out the one specified in the program. Some programs predefine kinds of types. But inconsistency will always be your's. Second: putting numbers everywhere to approach reality (as statistics do) makes that we have to consider consistency: what make the unit ? to whom it is relevant ? and so on.
Then: does, putting together 2 amounts ? can make addition neutral in overall amount ? There are many more examples than the one well known, which consists to observe what means joining mass of fissible radioactive material in critical amounts. 2 amounts made of same may interact, react and transform or can mean different things to active observers. This is just chemistry (and what drives quantities operations in chemistry is not simple operations but "Law of Mass Action").
1+ 1 barelly = 2
Of course, people knowing their environment know enough not to make or dispose something not at purpose: they have they sensible experience. Start to mind if it could behave in a different way. For example, I can put together 2 pounds of flour from different bags. It will make a 2 pounds amount exactly, unless introduced time should consider that ants can take some away or rats ruin all. Could we have thougth that the abstract "time" was not neutral ? or do we have used a label, and abstract failing to consider intermediate operations, or a real one and expected it to be neutral? That is already a picture of complexity if you mind systematically that, behind an intermediate abstract there always can be something disturbing your operations. Ignoring something and let it acts makes discover ants (or whatever) and disqualify previous operation(s).
Flour amounts are not supposed to interact. Same appearence can contain "residual" differences. One pound corrupted with salt, the other with sugar, mixing them will do a 2 pounds bag and a great difference: the success or the failure of your pancake. Operations there mean another thing.
Operations are also betrayed by utility. Amounts take sense with threshold. There, we have to consider both the accounting unit and the relativity of threshold effect(s). Say the number of kilojoules one body requires per day. There is both the thermic amount as well as the daily need which are different and vary according body shape or time delay required for provision. If amount is far from enough and delay probably or possibly too long; operations on too small amounts will have a different sense. So a windows: the more or less narrow domain of work of operations. We can die of starvation as well as of indigestion, not "gross difference" ? - but yes to all others. Less in the former will make death sooner. Less in the latter will give you a break but you may die from another thing than indigestion but related like heart attack.
Of course you know all that for sure ? really ?
Indeed societies and civilisations have, of course, developped mechanisms that could qualitativelly care their systems of operations proceed. Money for example has been created to reflect social utility or could want to be taken as gauge for universal values. But many have died from forced monetarization (or no enough?). Much speculation has occured. Because values of ones could not be shared or could have too easilly made the calamity of others. Despite so many evidences, on strange complex effects, like non linearity (inflation-deflation), varying scales (parity, unequality), irregular regimes (instability, catastrophic cycles) added to good use of simple ways to conduct operations - have scarcely been cautiously managed in quantitative efforts. Only very slowly have emerge qualitative concepts about accounting to make usefully comparable the numbers produced globally, at last more when in moments of crisis, just mind parity purchase.
Examine and Qualify Quantifying System
In the small following diagrams like subsets of olicognograph we intented to join concepts of operations, togethers in pictures of geometric logics. An intent to show you sorts of implicit systems of operations.
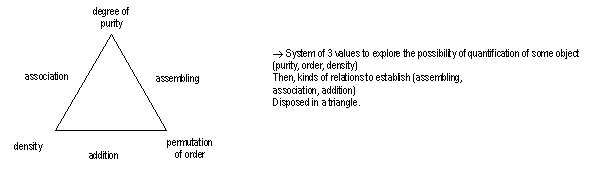
Our purpose is more pictorial and for conceptual flexibility: to open your mind. There are indeed more serious scientific ways existing in mathematics or fundamental physics to describe operations and nature of amounts. Our diagrams help to explore experimentable quantified behaviors, to examine in special sort of algebras.
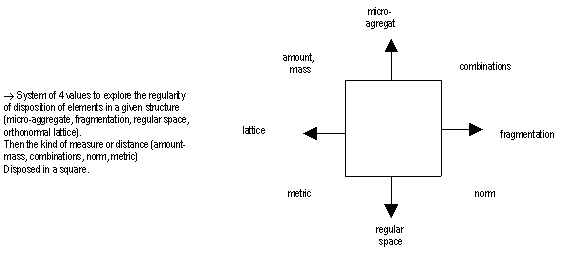
Our purpose is also to look pedagogically at some terms and operations which are uncommon to many common citizens but which identification could be good to learn to manage. Giving them a sort of lexic of terms you can explore.
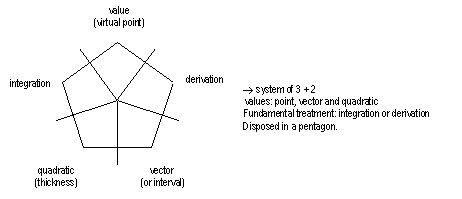
Knowing them, may help you to design or mind sort of terms and categories that are really universal (rather than just dialectic). That is they do not intent to impose a conclusion, a thesis but yes suggest subsets for "informal quantization": not a proper concept of theory of set, which is essential to clean theories of numbers. But we hope that they can shape you operating practice.
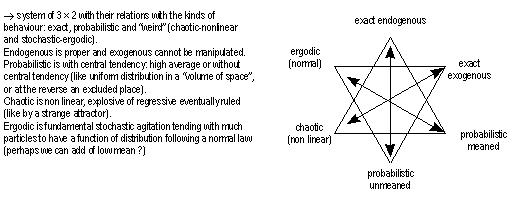
Practically
Mind complex duals: on simplest side the proper quantification of physics for engineering structural purpose or perfect brownian motion for perfect gas; on the complex ones ... the special graph algebra showing a logical frame of management of some issue. There are many applications of special algebra. Special algebras are not infinite and already used in fondamental physics (particles algebra, group theory in cristallography, etc.). The real way to science with numbers turns confused, mixed and harder (like in mathematics of fluid mechanics) but may locally apply useful mathematics to reality's as in biology, ecology and so on. There they give the ideas that things could be not so easy to determine.
At level of humane concern, there is both the fact that we have engineered material use of many things. These need precise algebras, some may inscribe in most universal one of real or complex numbers. Mathematics have also identified many complex situations that can be used in modelling and simulations. But they are social criteria at stakes that could use special algebra and others formalized partial mean (with better methods); to pattern sort of properties, criteria and concern, that should not be taken as scientific; just modelled cautiously under flexible umbrella of physics. Flexible umbrella because we have shown that technologically we can do many things.
Care not to call social calculus: "science"; we may use special forms, more fruitfully caring about:
- Democratic and consensus of special algebra, involving legitimacy and responsability not; lack of care and lazzyness
- Properties of special algebra, that could reflect social intentions, like balance, equity, asymmetries, corrections,
- Care more for effects of practice and diffused satisfaction rather than pretending unscrupulous unshared processes, be scientific according social theories: waste of public funds for academic ergotism.
